Алексей Шиндин
Алексей Шиндин
Как проверить модели и результаты их отображений на предмет несоответствий?
На примере системы интегрального подхода К.Уилбера - AQAL, которая представляет образец одной системы с подсистемами.
Простым языком, нужно выяснить
1. чего не хватает в карте, пропущено
2. что там лишнее и искусственно создано
3. какие несоответствия связей между элементам
4. возможно ли гибкое изменение системы с целями доработки
Любая система (или карта), которая предполагает наличие в ней всего, должна показать место и механизм отображения на любой предъявленный стимул. При этом возможны особенности, что
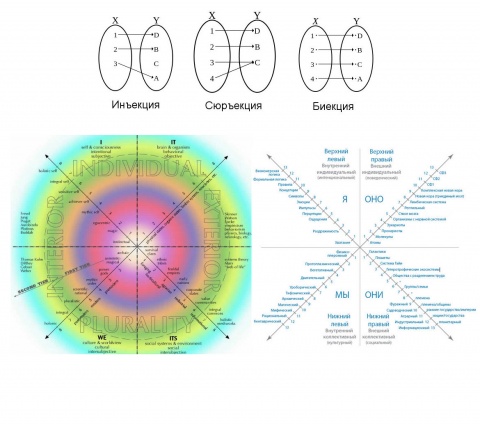
А1. каждый элемент системы имеет прообраз чего-то вне системы. При этом элемент системы может быть образом Анескольких элементов вне системы. Сюръекция.
А2. Каждый элемент вне системы имеет образ внутри системы. При этом часть элементов системы могут быть без прообраза, они ничего не отображают. Инъекция.
А3. И Биекция - когда одновременно и 1, и 2 - взаимо-однозначное отображение, когда вне системы соответствует системе.
А1. В случае "карт всего" сюръективные отображения могут быть проблемными, так как если мы уже имеем вне системы разные элементы, которые могут отображаться в один элемент системы. То есть поле системы уже уже отображаемой в нее области. Происходит потерять разнообразия.
А2. Инъективные отображения говорят о том, что в системе присутствуют элементы, которые на данный момент никак не представлены вне ее, за картой нет реальной территории. Они могут быть важными звеньями системы, но это неподтверждаемые на данный момент элементы, принять которые можно условно.
А3. И биективные отображения создают условия, когда любое предъявленное вне системы находит уникальное отображение внутри системы. Если это происходит всегда, то значит такая система способна к расширению. Если же это невозможно, то требуется пересмотр архитектуры самой системы.
Рассмотрим карту Интегрального подхода К.Уилбера Aqal, которая претендует на то, чтобы быть картой всего. Тут сразу у нас два варианта:
А. Карта всего как некоторой внешней реальности
Б. Карта сознания, которое все отображает и/или содержит
Хотя вариант Б работает в конкретном наборе философских парадигм (и не работает в других), именно он адекватнее характеризует суть систему AQAL. В этой системе есть принципы неисключения и включения-превосхождения, в том числе и поэтому она и претендует на карту всего.
Кроме того, предполагается, что наука будущего будет всеохватной и учитывать перспективы в разных секторах и интегрировать их в единое целое. Но чтобы это было возможным, сама наука для начала должна попадать хотя бы в один или несколько секторов. А все ли туда попадает?
Теперь давайте попробуем поискать ответы на пункты 1-4 в самом начале статьи, используя А1-А3 для потенциальной доработки или улучшения понимания.
Пример:
"Математика" - не совсем ясно, каким образом отображается в систему AQAL
Рассмотрим по-квадрантно:
ВЛ - математика тут либо отсутствует, либо должна быть субъективным, индивидуальным инструментом, что так же проблемно.
ВП - математика тут отсутствует, так как она хоть и частично помогает оперировать миром "внешниъ объектов", но занимается не только этим, и сама этим не является.
НЛ - математику можно считать языком как элементом культуры, но при этом она является больше чем языком. Она претендует на универсальный инструментарий и метод работы с ним. Кроме того, она занимается тем, чего вообще нет в культуре и вряд ли когда-то появится.
НП - трудно предположить, как попадает метематика в поле объективного-коллективного.
Поищем теперь математику в каждом сектор еще с двух позиций Интегрального постметафизического плюрализма. По представлению к.Уилбера можно выделить 8 зон и наборов методов в каждой из них.
ВЛ - феноменология + структурализм
ВП - ауэтопоэзис + эмпиризм
НЛ - герменевтика + этнометодология
НП - социальный аутопоэзис + теория систем
ВЛ - математика нефеноменологична и не относится к структурализму
ВП - не ауэтопоэзис и не эмпиризм
НЛ - как мы говорили выше, математика в некотором смысле является языком, поэтому герменевтична, но это не все ее функции.
НП - можно попытаться отнести математику к теории систем, но она по задачам и методологии к ним не относится. Более того, тут возникают трудности с понятием "теории систем", которые включены в AQAL. AQAL - это сама система, которую нужно исследовать во взаимодействии с другими системами, однако она пытается их включить в себя. Здесь возникает некоторый предел...
Предположительно математика не попадает полностью ни в одни из секторов AQAL, с возможностью частичного проявления в некоторых из них, которые при этом не отображают ее содержание. Но как отобразить математику в карте интегрального подхода AQAL?!
Заметим, что математика оперирует "идеальными объектами", а элементы для отображения таких объектов, предположительно, отсутствуют в AQAL, для них нет и отдельной зоны-сектора.
Математика сама является системой, которая так же может претендовать на описание всего. Получается, что мы имеем дело с разными системами и пытаемся отобразить одну из них через другую, и получаем неоднозначности такого отображения, так как когда мы работаем уже со множеством систем. Интегральный подход К.Уилбера будет частным случаем одной из систем, который все рассматиривает как свои элементы и подсистемы, к примеру, холархии. Холархия - это метод представления множества систем, но как подмножеств одной мета-системы.
Нам же необходимы возможности работы с многими системами, которые не сводятся одна к другой, обладают уникальным многообразием, а также интересны взаимодействия между, сохраняя эти уникальности. Для таких сложных задач мы можем переходить на другую логику моделирования, мышление и принципы работы, и это выходит за рамки методологии одной системы и приводит нас в миры многих мета-систем. К примеру, методологии Мозаичного мета-интегрального подхода.
Давайте поищем, что вы сумели найти в AQAL с возможностью доработки или улучшения понимания.
1. чего не хватает в карте, пропущено
2. что там лишнее и искусственно создано
3. какие несоответствия связей между элементам
4. возможно ли гибкое изменение системы с целями доработки
p.s. дополнения, возражения и указания на ошибки принимаются
Коментариев
Обсуждение интегрального подхода AQAL
Обсуждение в Январе-2013 членами российского интегрального сообщества сложных вопросов по интегральной теории AQAL
Комментарии к слайду
Нет комментариев